Edizione 2023 e 2024
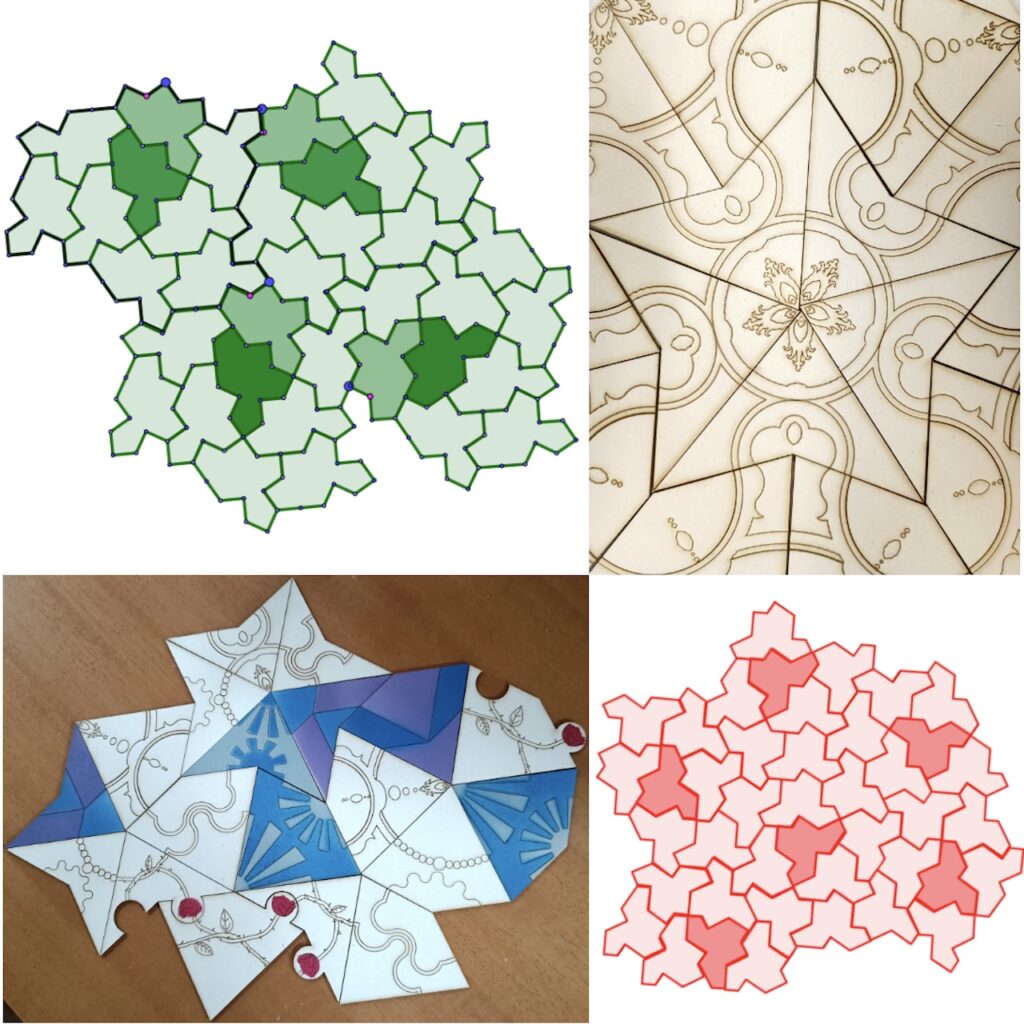
Tassellazioni non periodiche: uno è meglio di due!
venerdì 27 settembre 2024 – ore 19:00-24:00
Stand non stop – Via della Vasca Navale 109
Uno è meglio di due! Quando si parla di tassellazioni non periodiche (modi di ricoprire il piano con una o più figure geometriche ripetute all’infinito senza sovrapposizioni e non invarianti per traslazioni) viene subito da pensare ai due quadrilateri (l’aquilone e la freccia) di R. Penrose del 1974. Quasi 50 anni dopo, nel marzo 2023, i matematici D. Smith, J. S. Myers, C. S. Kaplan e C. Goodman-Strauss hanno presentato “An aperiodic monotile”, un preprint con una tassellazione non periodica con un singolo tassello di 13 lati, usato però necessariamente da entrambe le facce. Il 28 maggio 2023 gli stessi autori hanno mostrato che un solo tassello, senza ribaltamenti, è sufficiente per tassellare non periodicamente il piano. Forniremo i tasselli per i tre diversi casi (progettati e sviluppati nel Laboratorio Modelli e Prototipi del Dipartimento di Architettura di Roma Tre), chiedendo ai partecipanti di costruire le proprie tassellazioni. Alla fine, ognuno andrà via con un tassello ricordo.
Referente dell’attività: Corrado Falcolini – Dipartimento di Architettura
Barbara Licia Mauti – Dipartimento di Architettura; Matteo Siccardi – Liceo Socrate e Antonello D’Angeli – Liceo L. Rocci
Edizione 2021
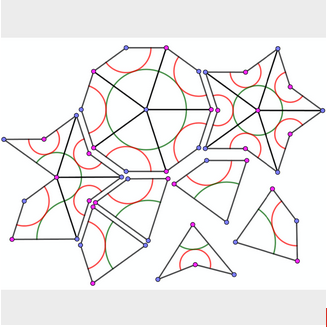
Costruire una tassellazione aperiodica di Penrose
venerdì 24 settembre 2021
Nel 1974, il celebre matematico Roger Penrose tornato all’attenzione del grande pubblico per aver vinto il premio Nobel 2020 per la fisica grazie ad un suo pionieristico lavoro sui buchi neri, scoprì le tassellazioni che da allora portano il suo nome. Ma cosa sono? Una modalità di ricoprire un piano con moltissime copie di pochi tasselli: figure geometriche che, senza sovrapporsi o lasciare buchi, si possono disporre all’infinito. Durante il laboratorio online, si vedrà come realizzare due tasselli che, combinati insieme seguendo poche semplici regole, permettono di realizzare una tassellazione non periodica, quindi sempre diversa rispetto alle molteplici scelte possibili: la costruzione geometrica dei tasselli sarà sviluppata con il software GeoGebra. Verrà mostrato, inoltre, come realizzare un’applicazione per simulare la costruzione della tassellazione. Infine, sarà mostrato come produrre i tasselli utilizzando una macchina a taglio numerico.
Corrado Falcolini – Dipartimento di Architettura e www.formulas.it